Théorème des valeurs intermédiaires
ILe théorème des valeurs intermédiaires et ses corrolaires
Soit \(f\) une fonction continue et monotone sur un intervalle \([a;b]\), alors \(f (x)\) prend toutes les valeurs entre \(f (a)\) et \(f (b)\).
En particulier :
Soit \(f\) une fonction continue et monotone sur un intervalle \([a;b]\), alors si \(f (a)\) et \(f (b)\) n'ont pas le même signe, alors l'équation \(f (x)=0\) possède une unique solution sur \([a;b]\).
Soit \(f\) une fonction dérivable sur \([a;b]\) telle que \(f'(x) \gt 0 \) (ou \(f'(x) \lt 0 \)), alors si \(f (a)\) et \(f (b)\) n'ont pas le même signe, alors l'équation \(f (x)=0\) possède une unique solution sur \([a;b]\).
IIApplication du théorème
On considère la fonction \(f\) définie par \(f (x) = x^3 - 12 x + 1\) sur \([3;4]\).
On cherche à résoudre l'équation \(f (x) = 0\) (ou au moins donner une solution approchée).
On va procéder de la manière suivante :
- Calculer la dérivée et étudier son signe (pour constater que \(f'(x) \gt 0 \) sur \([3;4]\)).
- Vérifier que \(f (3)\) et \(f (4)\) sont de signes contraires.
- Il sera alors possible d'appliquer le TVI pour prouver l'existence d'une solution unique
- On donnera un encadrement de la solution à \(10^{-2}\) près
1Calcul de la dérivée et étude de son signe
On dérive \(f\) et on obtient \(f'(x)=3 x^2 - 12\)
f'(x) est un polynôme du second degré, on calcule le discriminant : $$\Delta = b^2-4 a c = 0 - 4 \times 3 \times (-12) = 144 \gt 0$$ Il y a deux solutions \(x_1 = -2\) et \(x_2 = 2\)
Tableau de signe de \(f'\) : $$ \begin{array}{c|ccccccc} x & -\infty & & -2 & & 2 & & +\infty \\\hline f'(x) & & + & 0 & - & 0 & + & \\ \end{array} $$ Donc \(f'(x) \gt 0\) sur \([3;4]\)
2Vérification des signes aux bornes
Calcul de \(f (3)\) et \(f (4)\) :
$$f (3) = 3^3 - 12\times 3 = -8$$
$$f (4) = 3^3 - 12 \times 3 = 17$$
Donc \(f (3)\) et \(f (4)\) sont de signes contraires.
3Application du TVI
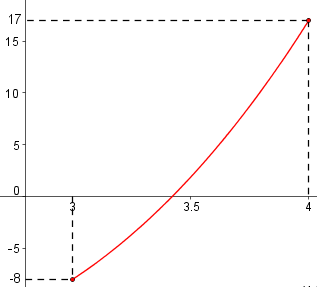
Comme on a démontré que \(f\) est une fonction dérivable sur \([3;4]\) telle que \(f'(x) \gt 0 \) et que \(f (3)\) et \(f (4)\) n'ont pas le même signe, les hypothèses du TVI sont vérifiées. En conséquence, l'équation \(f (x)=0\) possède une unique solution sur \([3;4]\) (voir la figure ci-dessous).
4Approximation de la solution
On note \(\alpha\) la racine de \(f\) sur \([3;4]\). Il faut utiliser le tableur d'une calculatrice graphique afin d'encadrer la racine par balayage.
- On choisit la précision souhaitée, par exemple le dixième (à \(0,1\) près).
- Tant que l'encadrement n'est pas assez précis, on ressère les bornes de l'encadrement de dixième en dixième (notons les \(a\) et \(b\)) de manière à ce que \(f (a)\) et \(f (b)\) soient de signes différents (on reste de chaque côté de la racine)
À l'unité près :
| Tableur : \( \begin{array}{|c|c|} \hline \ x\ & f (x)\\\hline 3 & -8\\\hline 4 & 17\\\hline \end{array} \) | La fonction \(f\) passe d'un nombre négatif à un nombre positif entre \(3\) et \(4\), donc : $$ 3 \lt \alpha \lt 4 $$ |
Au dixième près :
| Tableur : $$ \begin{array}{|c|c|} \hline \ x\ & f (x)\\\hline 3,4 & -0,496\\\hline 3,5 & 1,875\\\hline \end{array} $$ | La fonction \(f\) passe d'un nombre négatif à un nombre positif entre \(3,4\) et \(3,5\), donc : $$ 3,4 \lt \alpha \lt 3,5 $$ |
Au centième près :
| Tableur : $$ \begin{array}{|c|c|} \hline \ x\ & f (x)\\\hline 3,42 & \simeq -0,383\\\hline 3,43 & \simeq 0,19\\\hline \end{array} $$ | La fonction \(f\) passe d'un nombre négatif à un nombre positif entre \(3,42\) et \(3,43\), donc : $$ 3,42 \lt \alpha \lt 3,43 $$ |